磨矿介质的运动学

作用于钢球的力和钢球的运动状态

球磨和棒磨，都是由筒体转动使内部装的磨矿介质发生运动，因此对矿石产生磨碎作用。它们内部装的磨矿介质的运动，有很多相似之处，钢球的运动状态已经研究得比较充分，所以选它作为代表来作说明。既然磨矿作用是钢球运动产生的效果，所以研究钢球的运动学的目的，就在于对磨机的生产率，消耗的动力和最佳的主要磨矿条件等作根本性的探讨。

图3-4-1磨机内部装的钢球的运动状态（!）—泻落式；（"）一抛落式；（#）—离心运转

研究磨机内的钢球运动拍摄的照片，可以归纳为下图中的三种典型状态：泻落式、抛落式和离心运转。

如果磨机的转速不高，全部球荷向上偏转一定角度，其中每个钢球都绕自己的轴线转动。当球荷的倾斜角超过钢球在球荷表面上的自然休止角时，钢球即沿此斜坡滚下。钢球的这种运动状态，叫做泻落，如图3-4-1中的（！）。在泻落式工作的磨机中，矿料在钢球间受到磨剥作用。如果磨机的转速足够高，钢球自转着随筒体内壁作圆曲线运动上升至一定高度，然后纷纷作抛物线下落。钢球落下的地方，叫底脚区，其中的钢球强烈地翻滚。这种运动状况，如图3-4-1中的（"），叫做抛落。在抛落式工作的磨机中，矿料在圆曲线运动区受到钢球的磨剥作用，在底脚区受到落下的钢球的冲击和强烈翻滚着的钢球的磨剥。倘若磨机的转速高到超过某一临界值，钢球就贴在衬板上不再落下。这种状态叫离心运转，如图3-4-1中的（#）。发生离心运转时，矿料也是贴着衬板的。以上这些情形，都是指磨机内装有一定数量的钢球说的。要是磨机内只有少量的球，它们只是在磨机内的最低点摆动，并不发生上面讲的三种情况。用拍摄磨机内的介质的运动状态来研究它的运动规律，本世纪的二十年代已经开始，豪尔太恩、戴维斯、列文逊和我国的王仁东，都先后做过这方面的工作。

钢球作泻落式运动的力学尚缺乏研究，以后只讲抛落式的。

再详细地看看下面几张关于抛落式和离心运转的照片。

这些照片给我们一个深刻的印象：磨机内的钢球，发生抛落式运动或离心运转以及钢球的抛落高度等等，既决定于磨机的转速，也决定于装球量。在转速为临界值的 75%时，装球愈多，钢球的抛落高度愈大。在转速等于临界值时，装球率在40%以上才会发生离心运转。这些印象，使我们在分析钢球的运动时，必然把球荷重量和钢球运动时的离心力作为出发点。

将前面的磨机作抛落式工作的照片简化为图3-4-4，略去了底脚区，并且假定球作抛物落下的落回点就是它作圆曲线运动的开始点。

钢球在磨机内运动时，会产生沿着衬板下滑的相对运动。但戴维斯（"!#$%）拍摄的照片说明，如果磨机内只有钢球和水，下滑现象很明显，钢球不能上升到理论上它应达到的高度。倘若加入砂子，滑动现象即消除。有的试验指出，当磨机内只有钢球不加水和矿石时，球荷为10%、20%及30%都有滑动现象，球荷在40%以上时，滑动即停止。球荷有滑动时的力学分析，R . T.胡基作过研究，H. E.娄斯（Rose）和 R . M . E.苏利范（ Sullivan ）也作过探讨。以后所讲的磨矿介质运动学，基本上属于戴维斯的不涉及钢球滑动的范畴。此理论不考虑球荷的摩擦特性，忽略了同一球层中球与球的相互影响，也忽略了各球层间的相互干扰，而且许多公式都是近似的。这些缺点必然引出一些新的研究，但它们还不够成熟和完整，而生产中绝大多数磨机的情况大致与戴维斯的理论相符合，因此它仍然是有关磨机计算和开展新的研究的基础。

如下图，在球荷中任意取一钢球A!,它处于球的重量"的作用下，并且有离心力 C。G的切向分力T（ T = G sin a）使质点A!沿切线方向运动；G的法向分力& = cos!在第"和第#象限与离心力C的方向相同，在第$象限与C的方向相反。C与 &的合力的反力，配合上与AI接触处的摩擦系数（y）,构成摩擦力F，它的方向与 T力的相反，阻止T力沿切线方向运动。当钢球与筒壁没有相对运动的情况，T力和 F力是相等的。钢球受力C和力&压着，与磨机成一整体，随磨机以同样的线速度〃作圆曲线运动上升到A3点。在此处，力C和力&的大小相等方向相反，F = 0，切线分力T为后面的球上升时的推力所抵消。于是，钢球脱离筒壁，成为自由的，像与水平线成一角度并以速度〃抛出物体那样，受自身重量的作用，作抛物线下落。

当磨机转速过高时，球上升到了顶点，但离心力C比钢球重量G大，钢球就不会下落，发生了离心运转。

当转速较低时，不到A₃点，&力与C力已经相等，钢球即作抛物落下。&力与球的重量及球的位置有关，C力与球的重量和磨机转速有关，因而钢球能够上升到的高度决定于球荷及磨机转速，以后对此还要作详细说明。

球荷中的每一个球，都受到大小相等方向相反的T力和F力形成的力偶的作用, 因此都是围绕着自身的轴转动的，如图3-4（*）表示的情况。

二、球磨机的临界转速

(一）临界转速转速率

前面讲的，当磨机以线速度〃带着钢球升到A点时，由于钢球重量G的法向分力 &和离心力C相等，钢球即作抛物落下。如果磨机的速度增加，钢球开始抛落的点也由公式（4-3）可以看出，使钢球离心化所需的临界转数，决定于球心到磨机中心的距离。最外层球距磨机中心最远，使它离心化所需的转数最少；最内层球距磨机中心最近，使它离心化所需的转数也最多。如果取磨机内半径用公式（4-3）算的结果作为磨机的转速，尽管最外层球已经离心化了，但其他层球仍然能够抛落，还是可以磨细矿石。只有转数比用最外层球按公式（4-3）求得的高出很多时，全部球层才会离心化，磨碎矿石的有用功才等于零。但是，装入的钢球希望全部能落下磨碎矿石, 如果有一部分离心化，就会使有用功减少。因此，取磨机内半径用公式（4-3）算得的结果，说明要使最外层球也不会离心化时磨机转速的限度，就没有必要去计算使其他层球离心化的磨机转数了。由此可见，磨机的临界转数，是使最外层球也不会发生离心化的最高转速（转/分）。

尽管公式（4-3）是在没有考虑装球率及滑动等情况下导出的，但在采用不平滑衬板及装球率占40 & 50%时，它仍然符合实际情形。因此，生产中都采用公式（4-3）来计算磨机的临界转数，绝大多数磨机的转速都没有超过它。

（二）超临界转速运转

前面导出临界转数公式时，曾设摩擦力与钢球重量的切向分力相等，钢球没有滑动。在采用不平滑衬板和装球率占40 & 50%时，这种假设是符合实际的。倘若采用摩擦系数小的平滑衬板，又减少装球量使正压力降低，那么，摩擦力就小到不足以平衡球荷的切向分力，钢球于是有了滑动。在这种情况下，尽管磨机的转速超过用公式（4 -3）算得的好儿倍，因为钢球有剧烈的滑下运动，它还是不会离心化。这就是磨机超临界转速运转的实质和必要的条件。R . %,胡基在六十年代的研究指出，在适当
的条件下，磨机的转速超过！"值的20倍，钢球还不会离心化，仍然有磨矿效果。

超临界转速运转不仅在理论上突破了公式（4-3）的局限性，而且可以提高磨机的处理能力。生产实践指出，如果应用恰当，超临界转速运转可以提高磨机的生产力, 虽然功率耗相应地增加，但比功率耗（即千瓦•时/吨）常常是降低的，如下表中的例子。

表3-4-1南芬选矿厂提高磨机转速的工业试验结果

指标	第一段			第二段
球磨机实际转数（转/分）	24	26	30.5	21.5	26	30.5
转速率+）	85	93	108	75.5	93	108
装球量（吨）	13.0	11.5	10.0	13.5	10.5	10.0
球荷充填率（%）	41.1	36.4	31.8	42.7	33.2	31 . 8
球磨机利用系数（吨/米³ •时）
1）按原矿计	3.49	4.0	4.46	2.54	2.73	2.69
2）按-200网目计	1.11	1.47	1.52	1.05	1.44	1 . 25
利用系数变化（% ）
1 ）按原矿计	100	114.4	127.5	100	107	106
2）按-200网目计	100	124	131.0	100	137	119.0
比功耗（千瓦•时/吨）
1 ）按原矿计	5.33	4.95	4.83	5.55	8.3	7.17
2）按-200网目计	16.19	13.5	14.0	13.5	13.5	15.4
比功耗变化（% ）
1 ）按原矿计	100	93.0	91.0	—	—	—
2）按200网目计	100	83.5	86.5	一	一	—

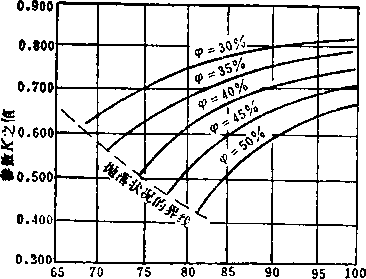
磨机的转速和装球量是影响磨机生产率的两个关键性的因素。超过！"值运转固然可以提高磨机生产率，但要求减少装球量，而减少装球量又会使生产率降低。所以不能片面地采用大幅度提高转速及大幅度减少装球量的办法，这反而会使生产率下降, 如下图3-4-6反映的情况。当装球率减少到25%以下，即使将转速率提高到145%，生产率也达不到装球率为35 - 40%而转速率为110-120%的。并且转速太高，磨机振动很厉害，也会造成危险。

要把磨机的转速提高到超过临界值，必须考虑原用的电动机的功率是否充足，传动部件的强度是不是够。磨机转速提高后，生产率加大，和磨机构成闭路的分级机的负荷也增加，必须采取措施提高分级机的生产能力和效率，要不然由于分级机的限制, 效果未必好。超临界转速后，钢球与衬板之间和钢球与钢球之间有强烈的相对运动, 磨损很厉害。为了解决这个问题，有用合金钢制衬板和钢球的，也有采用矿石自衬自磨的。试验研究和生产实践都指出：用普通磨机在超临界转速下进行矿石自磨，它的生产率可以达到在兀"以内用钢球磨矿的。衬板为特殊形状，由矿石自己去填补成一层壳，以便节约钢材。

超临界转速运转的磨机毕竟少见，即使有，多属小型磨机。唯独在芬兰，R . T. 胡基不仅作过系统试验和理论探讨，他们还曾用2700 -3600毫米球磨进行在超临界转速下矿石自磨的生产。

三、钢球的运动轨迹和转速率与装球率的关系

抛落式工作的磨机磨细矿石的效果，决定于它的转速率，装球率和二者的关系, 显然这些都是与钢球的运动有关。为了解决这些问题，必须从分析钢球的运动入手, 在明确它们的运动轨迹的基础上，逐步阐述怎样正确地选择转速率和装球率。

这就是在坐标中的球作抛物落下的抛物线方程式。

抛物线上各特殊点的坐标

为了使抛物线能够准确地画出，必须确定它的最高点'、它与#轴的交点和落回点B等的坐标。确定点的坐标：因"最大，故将公式（4-7）取一次导数并令它等于零，可以找出'点的坐标汇和。

脱离点与落回点的轨迹最大脱离角与最小球层半径

1. 脱离点与落回点的轨迹

磨机中的球荷由若干层球组成，每一层球都有一个脱离点和一个落回点"注每一层球的'，点的坐标各不相同，但它们既然都是脱离点，就都具有相同的几何条件。同样，各落回点B,的坐标尽管也不相同，但也都符合同一个几何条件。找出这两种几何条件，就找出了这两种转折点的连线，即脱离点与落回点的轨迹。

2. 最大脱离角和最小球层半径

由上图显然可知，愈近磨机中心的球层，它的脱离点轨迹和落回点轨迹愈靠拢, 到了磨机中心0处即汇于一点。从现象上看，愈靠近磨机中心的球层，它的圆运动和抛物线运动相互干扰愈厉害，以致二者几乎不可分。因此，最内球层的半径％ &必有一极限值，小于它，球层即无明显的圆运动和抛物运动。这个极限值叫做最小球层半径（%最小），可将它导出如下。

根据上面讲的情况可知，为了保证最内层球也能处于抛落状态（即所有球层都是抛落的），装球率与转速率必有一确定关系。而且这种关系又必有临界点，过了这种临界点，磨机的转速不足以使最内层球作抛落，钢球于是处于泻落状态。这里只将用计算结果绘制的曲线表示如下图。图中表明了装球率、转速率和球层半径的关系，也表

1. 磨机内的各区域与球荷切面积

(1)磨机内钢球分布的区域和各区域的磨矿作用在详细地分析磨机内钢球的运动规律之后，确地画出，如图3-4-10。从图中明显地看出，

（1) 钢球作圆运动区——图中画实影线的部分，钢球都作圆运动，矿石被钳在钢球之间受磨剥作用。

(2) 钢球作抛物落下区——图中画虚影线的部分，表明钢球纷纷下落的区域。在钢球下落的过程中，没有磨着矿石，直至落到用落回点轨迹BB2表示的底脚时。钢球才对矿石起冲击作用。

(3) 肾形区——靠近磨机中心的部分，钢球的圆运动和抛物线运动已难明显地分辨。在未画影线形状如肾的区域中，钢球仅作蠕动，磨矿作用很微弱。当装球较多而转速又不足以使它们活跃地运动时，肾形区就较大，磨矿效果也较差。

(4) 空白区——在抛物落下区之外的月牙形部分，为钢球未到之处，当然没有磨矿作用。转速不足时，钢球抛落不远，空白区就较大。转速过高，钢球抛得远，空白区虽然小，但钢球直接打衬板会造成严重磨损，磨矿效果也差。

磨机内的分区不仅如此明显，而且能定量地计算出它们的范围，下面讲的球荷切面积可作说明。

免责声明：矿库网文章内容来源于网络，为了传递信息，我们转载部分内容，尊重原作者的版权。所有转载文章仅用于学习和交流之目的，并非商业用途。如有侵权，请及时联系我们删除。感谢您的理解与支持。